 Arithmetic
Arithmetic
On a previous page, you learned the Musa numerals and signs. On this page, we'll discuss the symbols needed to express basic arithmetic.
Addition
In English, we use + to separate numbers being added together, but when we enclose a total in a larger expression, we have to surround it with parentheses or brackets, as in [4+3]. In Musa, we simply enclose the addends - numbers or larger formulas - to indicate that they should be added together, with dots separating the expressions. Musa formulas also always start and end with dots. The brackets for addition are low:
| | [4 + 3] |
|---|---|
| | [4 + 3 + 2] |
These formulas are one-dimensional, or 1D: they're just a sequence of Musa letters in the order that you typed them. But as formulas get more and more complicated, it turns out to be easier to read them in two-dimensional or 2D form: the vertical dimension is used to show how the elements group together, in both the traditional notation and in Musa. A big advantage of Musa is that you don't have to typeset the 2D notation by hand - the font does it all by itself.
When a formula like this is displayed using a Formula font, the addition brackets go below the addends, connected by an underline, with verticals extending up to show the position. They kind of look like a barge.
| | [4 + 3] |
|---|---|
| | [4 + 3 + 2] |
You can see that the diagonal corners of the "barge" match the diagonals of the original 1D Musa. That's true of all the brackets in the Formula gait.
Subtraction
To indicate subtraction, we replace the space with the subtraction separator before the number(s) being subtracted. You can subtract individual numbers or expressions no matter where they are in the sequence, even first.
| | [4 - 3] | |
|---|---|---|
| | [4 - 3 + 2] | |
| | [4 - 3 - 2] | |
| | [-4 + 3 - 2] | |
Multiplication
Multiplication works just like addition, except that the brackets for multiplication are high. In 2D, they kind of look like a hipped roof:
| | (4 × 3) |
|---|---|
| | (4 × 3 × 2) |
Division
Finally, division replaces the space with the division separator before the divisor. As with subtraction, you can divide individual numbers anywhere in the sequence.
| | (4 ÷ 3) | |
|---|---|---|
| | (4 ÷ 3 ÷ 2) | |
| | (÷ 4 × 3 × 2) | |
Precedence
These four operations can be combined without fear of ambiguity (and without precedence rules).
| |
|---|
| ([4 - 3] ÷ [2 + 1]) |
| |
Exponentiation
On the last page, you saw how to write powers like 3² with a simple Break uniting a low base and a high power, in that order. That works fine if the base and exponent are both simple expressions like x² or √x.
But if either is more complicated, we use a different notation for exponentiation. It features opening and closing brackets and a separator between base and exponent. There are two versions: one when the base comes first, and the other when the exponent comes first. In both cases, the high brackets go over the base, and the low brackets go under the exponent. The verticals are taller than for the other operations, too.
| base exponent | exponent base |
Because it's always clear which is exponent and which is base, it can be used in cases where the exponent can't be written high, for example when it's a variable or an expression. But if the exponent is a number, we write it high.
| | (d+g)ⁿ | |
|---|---|---|
| | e^(b+1) | |
Here's a complicated example: the quadratic formula. I've used the letters p t k to represent the coefficients of the quadratic px² + tx + k = 0, whose roots are the solutions to the formula. The second version is in connected form, which you should find easier to read: there are lines from the separator going over the base and under the exponent, and the three brackets are all connected.
| |
|---|
| -t + √(t² - 4pk) 2p |
| |
| (It's not correct to use ± before the root, since both square roots are added - one of them just happens to be negative.) |
Logarithms
Logarithms use almost the same notation, as you might imagine. The base and anti-logarithm (the number whose logarithm you're looking for) are connected by a wave that goes over the base and under the anti-log, using the same three brackets. The difference is that anti-logs are then also enclosed in a spiral, to distinguish them from exponents. Anti-logs are never written high, either, as numeric exponents usually are.
| base anti-log | anti-log base |
| log₁₀(25) | |
|---|---|
| ln(s) | |
Imaginary and Complex Numbers
The two symbols are used as signs to spell +i and −i, the two square roots of -1. Traditional notation considers them to be factors, but Musa considers them to be signs, a slightly sparer notation. By convention, we consider to represent −i, but it doesn't matter. means the same as : by convention, favor the latter, with positive radial magnitude.
These signs are used both as prefixes in front of imaginary numbers, and as infixes connecting the real and imaginary parts of a complex number:
| | 9i | | -9i |
|---|---|---|---|
| | 6 + 9i | | 6 - 9i |
| | -6 + 9i | | -6 - 9i |
Function Notation
Names of Constants, Variables and Functions
As with the traditional notation, Musa uses words within expressions to spell the names of constants, variables and functions. Placeholder variables, as used for example in the quadratic formula above, are usually written with a single consonant, but names can be any length, and should be separated from numbers by a dot. Unlike most computer languages, Musa doesn't include digits in names, since they'd be read as vowels.
Four common constants have conventional abbreviations:
-
tor = 2π ≈ 6.28318, the ratio of the circumference of a circle to its radius - not its diameter! The abbreviation stands for circle, and the name derives from the Greek word τόρνος, for a turn (e.g. on a lathe). For a discussion of why Musa chooses 2π, or τ, for its circle constant, please visit Pi is Wrong and The Tau Manifesto .
pyth = √2 ≈ 1.41421, the square root of two, also known as Pythagoras' constant (whence the name).
oy = e ≈ 2.71828, the base of the natural logarithms : ex is its own derivative. The name honors the Swiss mathematician Leonhard Euler (eu is pronounced oy in German).
pen = φ ≈ 1.61803, the "golden ratio", which is the ratio of a to b such that a/b = (a+b)/a.
The abbreviation pen derives from its close association with pentagons and pentagrams.
Units of measurement are always written before numbers, separated by a dot (which implies multiplication), and not plural. Measurements usually use magnitude notation: they're real numbers, not integers. For example, kg 1°81 is how we write 81 kilograms.
| | kg 1°81 | 81kg |
|---|
Even better would be g 4°81, with the metric kilo- prefix folded into the exponent.
| | g 4°81 | 8.1e4g | (kg = e3g) |
|---|
Compound unit names may include the reciprocal sign for division, or a power:
| | 25 man-hours |
|---|---|
| | 88 square meters |
| | 90 km / hour |
For a look at a different system of units, visit the Janus Units page.
Function Arguments
Functions not only have names; they also have arguments, parameters being passed to the function. For example, the trigonometric functions sin(α) cos(α) tan(α) all require an angle α. In Musa, we write the angle right after the function name - with no space - inside tandem brackets. In 2D, the brackets join to form a cartouche:
| | sin(p) | |
|---|---|---|
| | tan(p+t) | |
By the way, angles are expressed in Musa as fractions of a full circle, not as radians or degrees. One full circle is called 1 Torit, abbreviated To (not to be confused with tor, the Musa constant equal to 2π). For example, an angle of π radians or 180° would simply be a Musa angle of ½ Torit, written or . The arguments to the trig functions are in Torits, so they already have the 2π built in. Instead of writing cos(π/3) = 1/2, we would write cos(1/6) = 1/2.
(Even though the words tangent and cosine are written with aspirated letters in English, and the a is æ, these functions are abbreviated with unaspirated letters and a central a, as in Latin, and the same is true of other functions, so that they are consistent across languages.)
When there are multiple arguments, we use dots between them:
| | max(p, t, k) |
|---|---|
| | pop(cat, black, Salem) |
| (a hypothetical function returning the number of specified animals of a specified color in a specified place) | |
| | nested functions: age(queen(England)) |
| | exit() - a nullary function |
Musa function notation is also used in many cases which traditional notation handles idiosyncratically, each with its own notation. For example, the combinatorial function n choose k is written .
| | 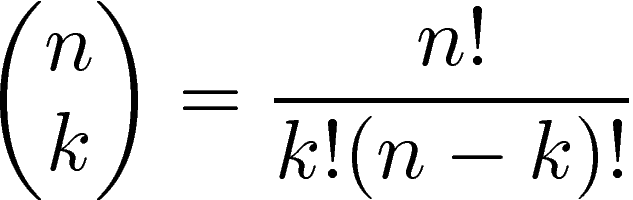 |
|---|
Sets, arrays, and tuples use the same brackets, with dots between elements. For example, we might say that the set of Heegner domains is:
| |
|---|
| [1 2 3 7 11 19 43 67 163] |
Procedures
There's another notation we're going to mention here without explaining it in depth, just so you've seen it. Most of the time, the functions written with the above notation don't have side effects: the parameters are passed by value, and the benefit - the reason you're calling this function - is contained in the return value.
But there's another type of function, one that encodes a transformation of its referent, and the return value - if any - may just report success or failure. This kind of function is sometimes called a procedure or a method. As an example of the difference, consider two small routines: one to tell you whether a particular window of your house is open, and the other to open a particular window. The first is a function: you tell it which window, and it tells you whether it's open without opening it. The second is a procedure: you tell it which window, and it opens it.
In the Musa notation for procedures, we put the referent (the object being transformed) before the function name, enclosed in brackets. In this case, the closing bracket is followed immediately by the function name, with no separation, and that's how you can recognize it. A procedure may also have parameters, and those are passed like in a function. It may also have a return value, just like a function. But a common trick is for a procedure to return its referent, so that procedures can be chained (like dot notation in object-oriented computer languages). To chain two procedures like that, just write the second after the closing bracket of the arguments of the first (those brackets may be empty).
For example, let's imagine you have a robot valet who takes care of your clothes. Its program might resemble this:
| |
|---|
| if isdirty(shirt) then (shirt)clean(gentle)dry()fold()hang() |
So if you see a function name preceded by brackets, you'll know it's a procedure.
Natural Arithmetic
In natural arithmetic, there are only positive numbers (including zero). The operators all use double (repeated) signs.
Absolute Value
A double negative sign indicates the absolute value of a number (the number without the sign):
| | |
|---|---|
| |-23| = +23 | |9.77| |
A double subtraction sign indicates the difference between the two numbers, which is always positive. For example, we say that New York is the same distance from San Francisco as San Francisco is from New York, not its negative.
| |
|---|
| |3-4| |
Modular Division
The two Modulo functions - quotient and modulus - are a variant of division. The main use of these functions is to perform conversions of numbers from one form into another: into integers, real numbers, or multiples of a modulus. The number being divided is called the dividend and the number of divisions is called the divisor. The result of quot is called the quotient, and the result of mod is called the remainder.
If the dividend and divisor are both natural numbers (positive integers, including zero), then the quotient and remainder are also both natural numbers, and the following three properties hold:
-
The quotient a quot b is always an integer
The remainder a mod b is always smaller (closer to zero) than the divisor b (unless the divisor is zero!)
The dividend equals the divisor times the quotient plus the remainder: a = b × (a quot b) + (a mod b)
For example, consider 7÷4. Using normal (real) division, the result is 1.75, and if you multiply the divisor by the quotient, you get the dividend: 7 = 4 × 1.75. But using modular division, the quotient would be 1 with a remainder of 3, and 7 = 4 × 1 + 3.
| | |
|---|---|
| 7 quot 4 = 1 | 7 mod 4 = 3 |
When the dividend and divisor aren't both natural numbers, the results are more complicated, but the same three properties always hold. When the divisor is negative, so is the remainder. When the dividend or divisor is real, so is the remainder. When the divisor is 1, the remainder is the fractional part of the number: 0 ≤ r < 1. When the divisor is zero, so is the quotient but not the remainder (and the division is valid)!
The two operations are used more often than you might think, for example for dates and times, or to separate numbers into integer+fraction, or real+imaginary, or larger+smaller than an arbitrary size. For instance, to truncate a number to the closest integer closer to zero, calculate n quot 1. If you want to know how many 8-packs of hot dog buns you'll need for five 6-packs of hot dogs, it's (5×6) quot -8 (the divisor is negative so the remainder is negative: leftover buns).
Equalities
Musa offers symbols for nine equalities, all written between spaces (unlike ). They all include a level accent.
The equals sign looks the same in Musa as it does in English:
| |
|---|
| 2 + 3 = 5 |
If the first number is greater than the second, we write:
| |
|---|
| 2 + 3 > 4 |
Likewise, if the first number is less than the second, we write:
| |
|---|
| 2 + 3 < 6 |
These last two are combined to form the symbol for unequal, that is, not equal:
| |
|---|
| 2 + 3 ≠ 4 |
They're turned over to form symbols for greater than or equal to and less than or equal to:
| | |
|---|---|
| 2 + 3 ≥ m | 2 + 3 ≤ n |
These last two are combined in the order ≥≤ to form the symbol for approximate equality, which is sometimes used as a general symbol for ambiguity.
| |
|---|
| √2 ≈ 1.414 |
The same two symbols are combined in the opposite order ≤≥ to form the symbol for equivalence, which means "not equal, but equivalent in some quality". For example, this is the relationship between the two square roots of negative 1. It might be used outside of arithmetic to match corresponding items, e.g. English cat ↔ French chat.
| |
|---|
| +i ∼ -i |
The equal sign is repeated to show when two expressions are identical, equal by definition:
| |
|---|
| ② ≡ -2 |
Finally, there are two symbols for assignment, which means "the value of the expression is assigned to the variable", or "the variable is being defined as this value". There are two versions, one assigning from right to left as is customary in computer languages (to highlight the variable on the left), and the other assigning from left to right in execution order (you have to calculate the value before assigning it).
| | |
|---|---|
| n ⇐ 5 | 5 ⇒ n |
Recap of Symbols
To recap, here are all the symbols (with zero standing for all the digits):
| | addition | | equal |
|---|---|---|---|
| | subtraction | | greater |
| | multiplication | | less |
| | division | | greater or equal |
| | function arguments, sets | | less or equal |
| | absolute value | | unequal |
| | difference | | approximate |
| | quotient | | equivalent |
| | remainder | | identical |
| | assignment | | |
| | exponentiation | | |
| | logarithm | | |
| | imaginary | | |
| | complex | |
That's all you need to write numbers and formulas in Musa!
If you're interested, the link at right below leads to a set of pages describing another number system, the balanced dozenal or Janus numbers, and a metric system based on them. They are an example of a very different numeric "language" that the Musa script enables. But you don't have to learn them to use Musa, any more than you need to learn Zulu or Inuktitut to write English in Musa.
| < Numerals | Janus Numbers > |
| © 2002-2025 The Musa Academy | musa@musa.bet | 19feb25 |