Musa has its own musical notation, based on the Janus number system. Janus is dozenal (base 12), and Western music uses a 12-note scale, so the homology is natural. Janus musical notation has the following advantages over the prevalent staff notation:

• Music can be written using the same symbols as language and arithmetic, on the same keyboard.
• Written music doesn't take any more vertical space on a page than normal text.
• Like a chromatic staff notation, intervals are written consistently: there are no "accidentals".
• It's easy to transpose.
• Rests use the same notation as notes.

To correctly display Janus musical notation, we use a special font: Guido Musa Partiture, named after Guido d'Arezzo, the 11th century Benedictine monk who invented solmization. Partiture is an anglicization of the word for sheet music in many languages.

Basic Notation

In traditional staff notation, the shape of a note indicates its duration, and its vertical position indicates its pitch. But Musa musical notation is written on a single line, so we indicate both the duration and the pitch of a note as a Musa letter: the top indicates the duration, and the bottom indicates the pitch. For both, we use the Musa shape corresponding to the appropriate digit. Here is a reminder of the Musa digits:

In Janus numerical notation, we don't use the digits        or their negative counterparts       , but we do in Janus musical notation.

Duration

In staff notation, durations are expressed as fractions of a bar or measure: we have whole notes, half notes, quarter notes, and so on. In 4/4 time, each measure is divided into four beats, and each is written as a quarter note. In 4/8 time, each measure is divided into four beats, but each is written as an eighth note - the music sounds the same, but the note length are halved.

In contrast, in Janus notation, we express the length of notes in terms of beats. In the same music as mentioned, we would say that four beats make up a measure (marked with a dot); in other words, that every fourth beat is a downbeat. And we'd say that each of those notes is one full beat.

The durations are written with digits corresponding to the number of beats. In 4/4 time:

• A Quarter note 𝅘𝅥 has duration 1 
• A Half note 𝅗𝅥 has duration 2 
• An Augmented Half note 𝅗𝅥 𝅭  has duration 3 
• A Whole note 𝅝 has duration 4 
• An Augmented Whole note 𝅝 𝅭  has duration 6 
• A Breve 𝅜 has duration 8 

We also use negative digits to represent durations one half beat shorter:

• An Eighth note 𝅘𝅥𝅮 has duration ½ 
• An Augmented Quarter note 𝅘𝅥 𝅭  has duration 1½ 
• A Half-plus-Eighth note 𝅗𝅥𝅘𝅥𝅮  has duration 2½ 

We also have some conventions:

• By convention, a Sixteenth note 𝅘𝅥𝅯, with duration ¼, is written as duration -7 . As a mnemonic, 1+6=7.
• By convention, a 32nd note 𝅘𝅥𝅰, with duration ⅛, is written as duration -9 . As a mnemonic, 3²=9.
• By convention, a vertical line duration  indicates that the previous duration is repeated.
• By convention, a tuplet is written using the zigzag duration  to indicate an "extra" note. For example, a triplet of quarter notes fills a half note's duration (the three triplet notes are each actually sixth notes: 3×⅙ = ½). Let's imagine they're the notes C E G. So we'd write the C under a zigzag to show that this series of quarter notes has an extra note, then write the E under a normal quarter-note duration, followed by the G under a vertical line - it's also a quarter note. Likewise, a quintuplet of five notes is written with a  above the first note, the nominal duration above the second note, and verticals above the other notes in the series.

Pitch

The pitch of the note is written with the digit corresponding to the number of semitones above (positive) or below (negative) the tonic, the base note of the scale of that key. This notation is chromatic, so there are twelve notes per scale, and no accidentals.

So for example, in the key of C, a C note is written as , a C♯ as , D is , and so on. Here's the C chromatic scale:

												
F♯	G	G♯	A	A♯	B	C	C♯	D	D♯	E	F	F♯

And in fact, the G chromatic scale, for example, is the same except that the bottom line is slid right or left:

												
D	D♯	E	F	F♯	F♯	G	G♯	A	A♯	B	C	C♯

This makes transposition very easy.

To write a rest - a note where no music is played - we use the digit  for the pitch value. A whole note rest would be written .

Since Janus digits range from -6 to +6, each pitch value can be expressed with only one digit, but that doesn't specify the octave. Sometimes, the composer leaves that to the performer, but if we want to determine the octave, we use the three accent marks       . We use the  Level accent to indicate that the note is in the same octave as the tonic, within the range of six notes lower to six notes higher. We use the  Rising accent to indicate that the note is in the next octave higher, and the  Falling accent to indicate that the note is in the next octave lower. If it's further than that, we can use multiple Rising or Falling accents. These accents are typed as full letters with a blank top before the digit they affect, and in the Guido font, they'll be displayed superimposed on the pitch. For instance, a Level accent  superimposed on a +5  is displayed as .

Chords are notes played together, and to spell them, we just write the pitch digits in a stack. To type that, just write the second and further pitches with a blank top, and the font will stack them. To make them easier to read, we always write the notes in pitch order, higher notes on top. For example, a C major chord is C E G, and we'd write it      - the  actually stands for the G above C, despite the negative digit.

Percussion

Things work a little differently for percussion instruments, which in general each only produce one pitch. However, the same drummer usually has numerous different instruments at hand: drums, gongs, tambourines, triangles, cymbals, hi-hats, cowbells, etc. - an entire battery. Janus percussion music thus has only the durations, but usually includes several parallel tracks.

Example

Let's put duration and pitch together to spell a simple melody, the Beatles And I Love Her. Here's a video.

The key is E major, but we only need to know that to read the staff notation, not to write the Janus. For now, I won't include the signatures at left or the chords above, just the melody for this one line:

Signature

At the beginning of a piece of music, we can declare the interpretations of both the beat and the tonic in absolute terms, by default in Janus units. They're assumed to apply until replaced, or until the end of the music.

The timing of a beat is preceded by the letter : a duration of 1, followed by a High Level Accent . Then we write the time between beats, followed by a low level accent . A rhythm of 120bpm - one beat per half second - corresponds to a frequency of 7.771e-7 Chronit, or  in Janus

The frequency of the tonic is preceded by the letter : a pitch of 0, followed by a High Level Accent . Then we write the frequency, followed by a low level accent . The frequency of middle C is 261.6Hz, which corresponds to 5.90596e-9 Sychnit, or  in Janus.

Rounding both numbers, we could write the signature of a piece at 120bpm in the key of C as .

Orchestration

Now comes the hard part! A piece of music isn't just the melody, it's also the other "voices". For And I Love Her, the melody above was played by George on lead guitar or sung by Paul. John played rhythm guitar, Paul played bass guitar, and Ringo played bongos and clave. All of those voices have to be written, and the notation has to show how they align.

In addition, they're not just all repeated till the end of the song. In And I Love Her, George starts off playing the famous guitar riff, but stops when Paul starts to sing. After one verse, he starts up again, but a different riff. After two verses, they switch to the middle eight, a completely different tune. After returning to the original melody for another verse without rhythm guitar, Paul stops singing for George's solo, which is followed by a key change. They follow that with a fourth verse, and then a short finale. All that has to be choreographed, and hopefully without repeating music as staff notation does.

The instructions that specify all that can be called the Orchestration. The columns are called sections, the rows are called voices, and each cell is called a part. The parts are numbered, and each line of music is labelled as a part. The parts are often written on the same page, with the measures lining up, but the orchestration is separate. Here's what it might look like:

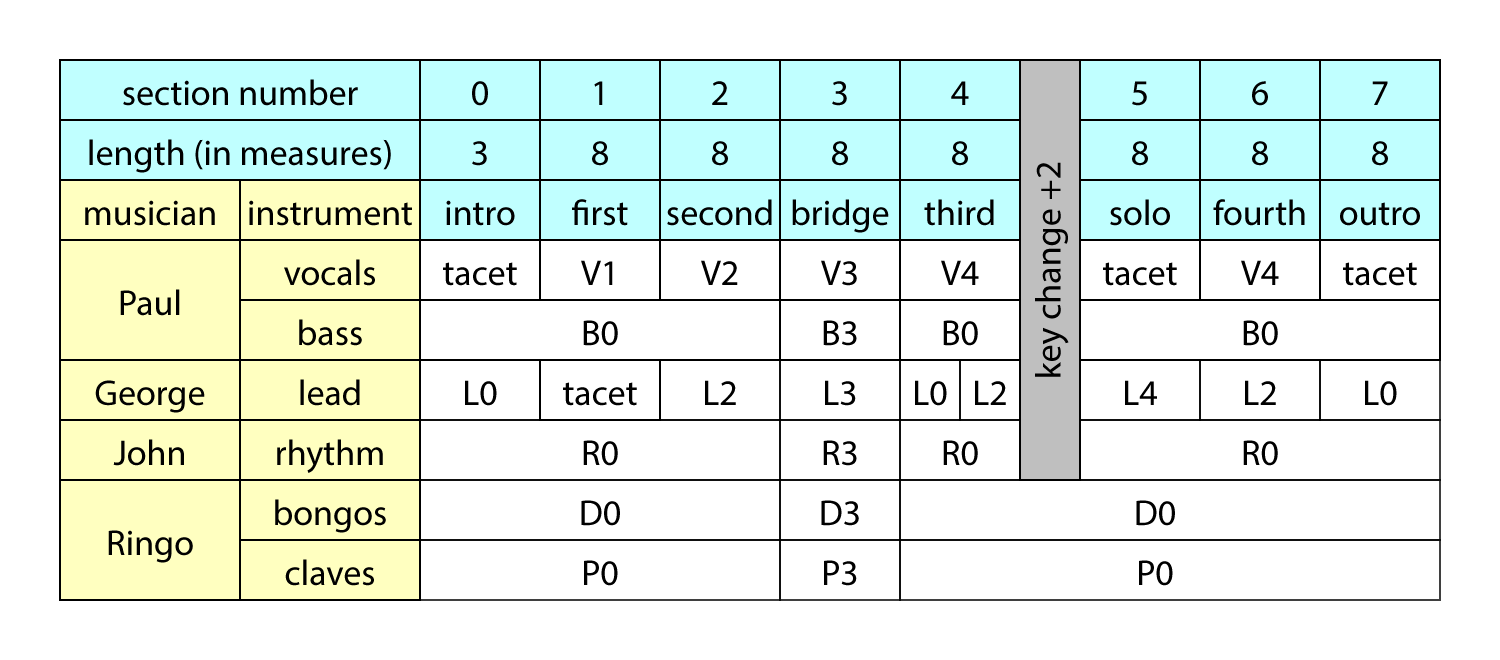
Now imagine the same for an orchestral symphony!

Adaptive Tuning

Adaptive tuning is something new that has been made possible by digital instruments. The idea is that instead of each note remaining at a fixed pitch until retuned, each instance of a particular note can be adjusted to harmonize perfectly with the preceding note, so there are no wolf intervals. The adjustments are usually tiny and not apparent to the ear unless compared directly, but the result is more harmonious. With adaptive tuning, the pitch of a note may simply vary around a value, or it may drift up or down over the course of a piece.

Here's a longer explanation: A plucked string will vibrate, and will produce a sound whose pitch depends on the length of the string (and many other factors). It will also produce overtones - secondary vibrations - at pitches corresponding to half its length, a third of its length, a quarter of its length, and so on. The half-length pitch is an octave higher than the original pitch. The two pitches harmonize, an effect that we humans find pleasant.

Likewise the quarter-length pitch is the original pitch, two octaves higher; it's half the half-length. But what about the third-length pitch? That one is in between the other two, in a ratio of 3:2 with the base note of its octave. For historical reasons, that ratio is called a fifth, and is the most important ratio within the octave: a C will resolve to a G. The inversion of the fifth, the pitch whose ratio is 2:3 - which is 4:3 of the octave above - is called a fourth. The fifth-length pitch is in a ratio of 5:4 with the base note of its octave, and that ratio is called a third.

By chance, the number 3¹² (531441) is very close to the number 2¹⁹ (524288), only 1.364% larger. If they were equal, then 6 steps of 9/8 would be 2/1, and evenly divide the octave, geometrically. As it is, we have to conceal that 1.364% somewhere in the progression. The different ways that's done are the different types of tuning. There are tunings with equal intervals between all 12 notes, and others with some intervals larger than others.

But once the tuning has been done, we ignore it and play the music, dividing the octave into 12 semitones with an average interval of about 106%. The problem is that equal semitones won't harmonize - they won't match each other's overtones. To do that, they need to have pitches in small ratios, like 3:2, 5:4 or 9:8. So normal scales use just tuning: the most-used intervals are small ratios. Here's the C Major scale with just tuning:

note	C	D	E	F	G	A	B	C
semitones	0	2	4	5	7	9	11	12
ratio	1:1	9:8	5:4	4:3	3:2	5:3	15:8	2:1
name	unison	second	third	fourth	fifth	sixth	seventh	octave

The ratio between C and D is 9:8, but the ratio between D and E, also successive whole tones, is 10:9! That's not good: we want equal intervals to be equal.

In adaptive tuning, we keep the interval correct and let the frequency follow. Here are the 37 intervals corresponding to the notes listed above, and their equivalents - their meaning - in ratio form:

semitones	-18	-17	-16	-15	-14	-13	-12	-11	-10	-9	-8	-7
ratio	5:14	3:8	2:5	5:12	4:9	15:32	1:2	8:15	9:16	3:5	5:8	2:3
semitones	-6	-5	-4	-3	-2	-1	0	1	2	3	4	4	6
ratio	5:7	3:4	4:5	5:6	8:9	15:16	1:1	16:15	9:8	6:5	5:4	4:3	7:5
semitones		7	8	9	10	11	12	13	14	15	16	17	18
ratio		3:2	8:5	5:3	16:9	15:8	2:1	32:15	9:4	12:5	5:2	8:3	14:5

Let's take a look at "Twinkle, twinkle, little star". The first two notes are C, at 261.6 Hz. The next two, the second "twinkle", are G, seven semitones above. Using the ratio above, we multiply 528Hz by 3/2 to get 392.4 Hz for this G. The A of "little" is at 441.5 Hz, 9/8 of 392.4 Hz. The G of "star" goes back to 392.4 Hz - 8/9 of the A - but the F of "how" goes to 348.8 Hz, 8/9 of 392.4 Hz. The E of "wonder" is only one semitone lower, at 327.0 Hz, 15/16 of 348.8 Hz, and the D of "what" is 8/9 of that, 290.7 Hz. And the final C comes out at 258.4 Hz! In the course of the line, the tonic has moved 1%, but the intervals are all small integer ratios.

Credit for help with this section is due to Alvin Wen.

< Janus Logic

Home >